-
FT Exploring
Energy Pages: - Wind Turbine Power Formula
- Don't Misuse Turbine Efficiency
- Energy Makes Things Happen
- Definition of Energy
- Types of Energy
- 1st Law of Thermo
- 2nd Law of Thermo
- Power vs Energy
- Examples of the First Law
- Examples of the 2nd Law
- SOLAR ENERGY!
- Energy is Everything
- PHOTOSYNTHESIS!
- Energy Flows through Life
- The Definition of Life
- Biology & Cell Metabolism
- What is ENGINEERING?
- Dr. Galapagos
- Site Map
- Links
- CONTACT ME
Wind Turbine Power Coefficient (Cp)
Power Coefficient (Cp) is a measure of wind turbine efficiency often used by the wind power industry. Cp is the ratio of actual electric power produced by a wind turbine divided by the total wind power flowing into the turbine blades at specific wind speed. When defined in this way, the power coefficient represents the combined efficiency of the various wind power system componenets which include the turbine blades, the shaft bearings and gear train, the generator and power electronics.
The Cp for a particular turbine is measured or calculated by the manufacturer, and usually provided at various wind speeds. If you know the Cp at a given wind speed for a specific turbine you can use it to estimate the electrical power output.
The Cp of a particular wind turbine varies with operating conditions such as wind speed, turbine blade angle, turbine rotation speed, and other parameters. It is a measure of a particular wind turbine's overall system efficiency. It should not be confused with, or compared to, wind power Capacity Factor.
As explained in the page on wind turbine efficiency, the power coefficient should only be used to compare the performance of wind turbines. Cp has no relationship to the efficiencies of other electrical power sources, such as solar, gas-turbine, a coal-fired steam plant, or any other non-wind driven system.
Power Coefficient - It's an Efficiency
I would like to call it (and some people do) overall turbine system efficiency. The wind power industry often calls it the Power Coefficient, and gives it the symbol Cp.
The technical and product literature is now full of it (the term Cp I mean), so Power Coefficient it shall be for the rest of this page.
Power Coefficient - An Indicator of Total Wind Turbine System Efficiency
The term Power Coefficient is commonly used to designate the efficiency of the entire turbine power system. As shown in the expression below, it is generally defined as the ratio of the "electrical power produced by the wind turbine" (Pout in the formula below) divided by the "wind power into the turbine" (Pin). Pin is sometimes also called "available wind power". But I don't really like that expression because the total power in the wind is never really totally "available".


Total Wind Power - A Function of Wind Speed Cubed

is a function of air density, rho
(funny greek letter above);
the blade swept area, A;
and the cube of the wind velocity, V.
The total wind power flowing into the turbine is defined by the fairly simple wind power formula, shown to the right. The power into the turbine blads is a function of the wind speed to the 3rd power (V times V times V), air density, and swept area of the turbine blades. A simple version of the wind power formula is shown to the right.
The symbol that looks like a backwards 9, is the greek letter, rho. Rho is often used to symbolize the density of a liquid or a gas. In this case, rho stands for air density.
The capital letter A represents the blade swept area. Note that for the most common horizontal axis turbines the swept area can be determined by the formula for the area of a circle which is Pi times the blade diameter squared (D^2 or D times D), divided by 4. Thus you may also see the formula written with D squared, as I show it on some other pages. (In that case you would also have the number Pi in the numerator and 8 in the denominator).
For a given turbine, the swept area is a constant, but the air density will vary with elevation and with barometric changes at a given site and, of course, both wind speed and direction will vary over time.
Electrical Power Produced - The End Result of Aerodynamic, Mechanical, & Electrical Efficiencies
Some wind turbines do things like pump water and grind grain. But most, and virtually all the big ones, are used to make electricity. If you are buying a wind turbine to make electricity then you are interested in the actual useful electric power your turbine will generate at a given wind speed.
In the adjoining text I say, "at each step, some energy is lost". It's how we engineers often talk about energy and power flow processes.
We should remind ourselves though, that the 1st Law of Thermodynamics (often called the Law of Conservation) tells us energy is neither created nor destroyed. When we talk about losing energy we just mean we've lost some of the useful mechanical or electrical energy we're trying to transmit to your house for things like washing clothes and making toast.
As described in my pages on the 2nd Law of Thermodynamics, the lost energy has flowed into the surroundings as low grade thermal energy. In other words, it heats up the air a little bit. It's "lost" to us, but it still exists.
The energy conversion process that turns wind power into electric power goes through 3 major conversion steps which I will label here as the aerodynamic, mechanical, and electrical conversion steps. At each step, some energy is lost (yup, it's the 2nd Law), and the final electric power is less than the total wind power we started with. (This is not unique to wind. All power systems have losses.)
Aerodynamic Efficiency - The wind power rotates the turbine blades, converting the wind's kinetic energy into the rotating mechanical energy of the turbine shaft. This is the first and largest "loss". The efficiency with which the blades convert available wind power to rotating shaft energy is sometimes referred to as aerodynamic efficiency.
You may have heard of the Betz limit which says the best a wind turbine can do is convert a little more than 59% of the incoming wind power into mechanical shaft power. In reality it is lower than that, and at most wind speeds, much lower (see graph below).
Mechanical Efficiency - In most of the large turbines, the turbine shaft drives a gear box which changes the blade's rotating speed to a speed that better suits the generator (usually faster for a big turbine). Even the best gear trains have friction and some energy is lost here. In addition there are large bearings supporting the shaft which also will introduce a little friction. Let's cleverly call the efficiency of all these mechanical components the mechanical efficiency.
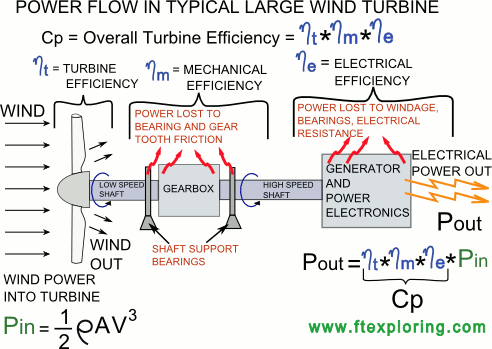
Electric Efficiency - The shaft out of the gear box turns an alternator or generator which converts the mechanical energy into electrical energy. At this point, the electricity can either be direct or alternating current, depending on whether it is a dc generator or an alternator. But even if it is an alternator, the frequency of the current is unsteady and will not match the exact 60 Hz (or 50 Hz in some countries) of the electric power grid.
Some complicated power electronics are needed to convert the much less-than-perfect electriciy into the clean & precise 60 Hz power needed for the grid. Both the generator and power electronics have losses also. Let's combine these two systems and refer to their combined performance as the electric efficiency.
As shown in the drawing above, Cp is a measure of the overall system efficiency of a specific wind turbine, combining the efficiencies of the blade rotors, the mechanical, and the electrical systems.
Let's do an example:
First, here is the symbol η. It is the small greek letter eta. We commonly use it to represent efficiency.
So let's designate the following symbols for our three efficiencies:
ηb = blade aerodynamic efficiency
ηm = mechanical efficiency
ηe = electrical efficiency
Then we can write the following to show that Cp is the combination of the efficiencies of all the subsystem components:
Cp = ηb x ηm x ηe
Okay, now I'm going to put some values in the 3 efficiencies. These numbers have some basis in reality, but don't come from any specific turbine. Don't go quoting them! It's just an example to illustrate that Cp, when used this way, is an overall efficiency of the whole system. Also, these are pretty darn good efficiencies. The assumption is the system is operating at, or near, maximum power, as well as near the best operating design point of the components.
Assume the following efficiencies for a large wind turbine, with the characteristics shown in the plot above:
ηb = 0.397 (39.7%, which, by the way, is pretty darn good aerodynamic efficiency)
ηm = 0.96
ηe = 0.94
Then,
Cp = ηb x ηm x ηe
= 0.397 x 0.96 x 0.94 = 0.358
Amazingly, 0.358 (or 35.8% if you prefer) is about the value of Cp in the chart below at a wind speed of 12 meters per second. It's not really amazing. Nor is it a coincidence. I fudged the numbers to make it come out that way. It's just an example of how to do the calculation!
Using the wind power formula shown above, with an assumed standard air density at sea level of 1.225 kilograms per cubic meter (kg/m^3), and a blade diameter of 101 meters (about 331 feet - pretty big), I can calculate that the wind power into the turbine, at 12 meters per second (m/s), is 8,480 kW.
Therefore we can easily calculate the actual electrical power produced by the turbine to be,
Pout = Cp x Pin = 0.358 x 8,480 kW = 3086 kW
The maximum power of the imaginary turbine for which the data is plotted below.
Power Coefficient Varies with Wind Speed and Other Variables
It should be obvious that a Cp of 1 (or 100%) is impossible. It would mean that all of the power (kinetic energy converted per unit of time) would be converted to electrical power. No wind coming out of the downwind side of the turbine and no mechanical or electrical losses in the system.
The sample calculation above represents a well designed turbine running at or near its most efficient operating point. So it should be clear that real turbines operate at a Cp of considerably less than 1.
Look now at my little chart below. It is a plot for a specific actual wind turbine of the Cp and Pout (actual electric power produced in kilowatts) versus wind speed (in meters per second).
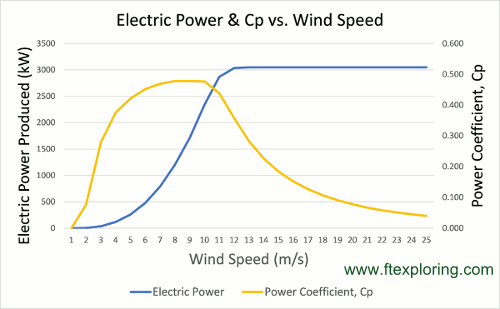
It's a useful plot with some interesting information (Remember, turbines vary, this is just one example. Each specific model will have it's own data):
First, notice that Cp (yellowish line in chart) varies significantly with wind speed. For this particular turbine, maximum efficiency occurs around the wind speed range of 8 to 10 meters per second (18 to 22 miles per hour). Other turbines may attain maximum efficiency at other speeds.
The blue line shows the electric power produced as a function of wind speed. When the turbine reaches maximum power, which in this case is 3030 kW, it levels off. This is because the turbine blades are turned, or feathered, to keep them from spinning too fast, or breaking from too much force. The turbine control system will keep the blades spinning at or near a constant value. Though it is not shown in the curve above, at some point the blades are stopped for safety, and power rapidly goes to zero.
For this particular turbine, the maximum efficiency starts to fall a little before maximum power. Once the system reaches maximum power the power coefficient starts to fall off rapidly. This is because the power is kept constant while the wind power into the turbine is increasing rapidly. Remember the power is a function of the wind speed cubed. Pout stays constant while Pin is increasing very fast. Cp has to get smaller.
Look at the plot below. The wind power into the turbine blades is shown by the gray line. Because it increases with the cube of the wind velocity, it is increasing so fast with increasing wind speed that it's hard to show the blue power produced line which levels off at 3030 kilowatts. To capture power above the maximum limit would just put too much stress on the blades and/or drivetrain components.
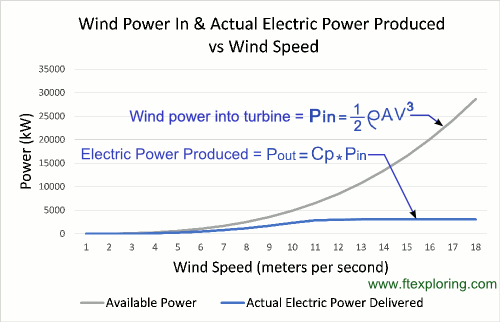
It also should be noted that manufacturers tend to specify Cp numbers that are based on certain ideal or standardized conditions. This is reasonable, since the numbers are helpful for comaparing to other turbines. However, in the real world, turbine blades get dirty, ice forms on them, and their surfaces wear or get otherwised damaged. The almighty wind, though freely available, can be capricious and gusty, changing direction and speed randomly and frequently.
All this means that turbines rarely operate at the exact Cp quoted by the manufacturer.
Summary
The term power coefficient is used by much of the wind power industry to represent the overall efficiency of the turbine. It combines the efficiencies of the blades, mechanical, and electrical components. Knowing the Cp at a given wind speed provides a simple approximation of what the actual electrical power produced by the wind turbine will be.
©Copyright 2015. David E. Watson. All rights reserved. Just about everything in the FT Exploring web site is copyrighted. For information concerning use of this material, click on the word Copyright.
Disclaimer: I know a fair amount and am more careful than most (not necessarily more humble), but I'm not infallible. Neither is anyone else. We can all be wrong, make a mistake, learn from our mistakes, and change our minds (except politicians, of course). If you are undertaking a real-world project, you are responsible for either knowing what you are doing, or getting help from someone who does. I would also talk to more than one expert. And for goodness sakes, know the difference between power and energy, get your units straight, and don't violate the 2nd Law of Thermodynamics (I've seen many inventors try during my career - so far they have all wasted theirs, and sometimes their investor's, time and money).

The "not-interrupting-content-as-promised", side links below, are personal recommendations from David Watson, who is wise and thoughtful:

Visit B Willard's
Lonesome Design Shop
This is fun! Great music. Great lyrics!
The best band you probably haven't heard of.

At Latal music available here - free even
(but generosity is good for your karma)



